The class for a linked binary tree structure is very similar to that for a linked list structure (again we will discuss just structures containing integers for simplicity):
class Cell
{
int item;
Cell left,right;
Cell(int n,Cell l,Cell r)
{
item=n;
left=l;
right=r;
}
}
Although we have called it Cell, the same name we called
the class for cells in linked lists, this will be no problem since we
will again make it a nested class within the class for sets.
The structure for the class that gives us sets will be as follows:
class IntSet13
{
// Destructive Set class, sets stored as ordered trees
private Cell tree;
code for the method delete
code for the method add
code for the method member
code for the method toString
code for the class Cell (i.e. as given above)
}
Given the class Cell as above, if we have variable declarations
Cell t1, t2, t3;after executing the code
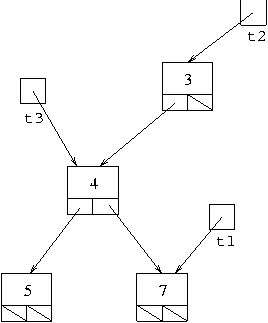
t1 = new Cell(7,null,null); t2 = new Cell(5,null,null); t3 = new Cell(4,t1,t2); t2 = new Cell(3,t3,null);for example, we will end up with a structure which can be shown in diagrammatical form:

As this example shows, although cells in a tree structure have two
link fields, it is possible for one of those links to be null
and the other not, leading to one outgoing link.
The exact shape of the boxes in the diagrams is not important. You might also see them drawn as:
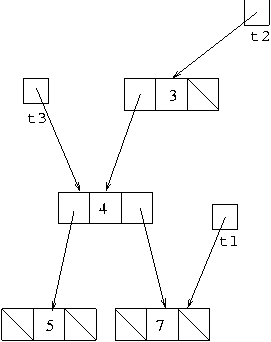
If it is not necessary to stress exactly how it is made up of cells and pointers, the tree may be shown more simply as:
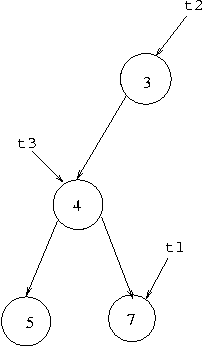
As with the linked list structures, the fields here are not declared
as private so it is possible to change them directly.
For example, suppose after executing the code above we executed:
t3.right.item=10;This would change the situation to that represented by:
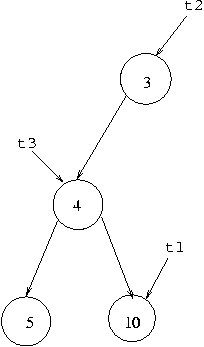
Note this means the tree referenced by t1 is changed because
the cell referred to be t3.right is the same cell as that
referred to by t1, and the tree referenced by t2
is changed because the cell referenced by t2.left is also the
cell referenced by t3.
Given a Cell object referenced by a variable t,
the structure referenced by t.left is referred to as the
left subtree of t, the structure referenced by
t.right is referred to as the right subtree of
t and the value in t.item is referred to as
the node value of t. It can be seen that a tree is
a recursive data structure, since it will either be the empty tree
(represented by null) or a tree made up of a data item
and two trees.
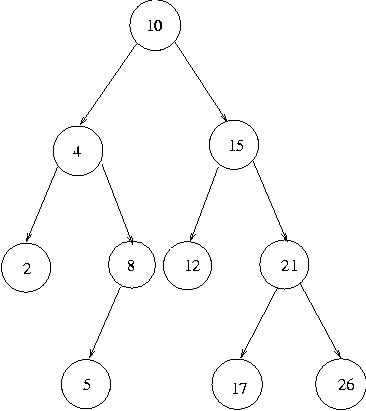
Ordered binary trees
A binary tree is ordered if it is the empty tree. It is also ordered if
both its subtrees are ordered and all the items in the left subtree are
less than the node value in the ordering used, and all the items in the
right subtree are greater than the node value. The tree below is an
example of an ordered tree:
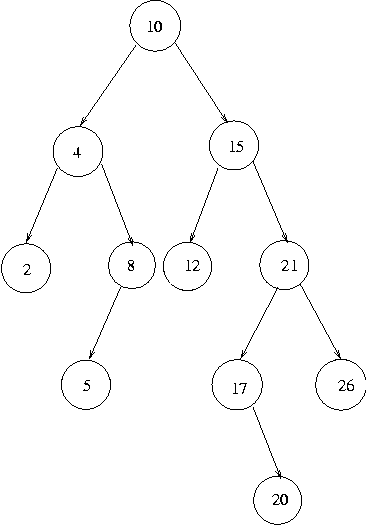
Now suppose we want to alter this tree to represent adding the number
20. To do so, we can note that 20 is greater than the node value, 10,
so we must add it to the right subtree. It is greater than the
node value of that subtree, 15, so we must add it to the right
subtree of that subtree. But it is less than the node value of that
subtree, 21, so we must add it to that subtree's left subtree. It is
greater than the node value of that subtree, 17, so we must add it to
that subtree's right subtree. As that tree is empty, we replace it
by a new tree whose node is the value being added, 20, and whose
subtrees are both null. This gives us:
So long as we always add new integers in this way, we will keep the
tree with its ordered property. We can represent this process of
moving down to the left or right subtree until one is reached where
the tree moved to would be null by the following code:
public void add(int n)
{
if(tree==null)
tree = new Cell(n,null,null);
else
{
Cell ptr=tree;
while(ptr.item!=n)
if(n<ptr.item)
{
if(ptr.left==null)
ptr.left = new Cell(n,null,null);
ptr = ptr.left;
}
else if(n>ptr.item)
{
if(ptr.right==null)
ptr.right = new Cell(n,null,null);
ptr = ptr.right;
}
}
}
The loop here will exit without any new cell being created if it
encounters a cell with node value equal to the number being added,
which is what we want for sets as we have defined them.
The code for testing membership of a set represented by a tree is
simple. We start at the root of the tree, and work down moving to
the left subtree if the number we are looking for is less than the
node value of the tree, to the right subtree otherwise, until we
reach a position where the pointer we are moving down either points
to a cell holding the number or has become null. In the
former case, the number is in the set, in the latter it isn't. Here
is the code:
public boolean member(int n)
{
Cell ptr=tree;
while(ptr!=null&&ptr.item!=n)
if(n<ptr.item)
ptr=ptr.left;
else
ptr=ptr.right;
return ptr!=null;
}
This shows the main advantage of using ordered trees to represent
sets of data. Each time we move down one branch of the tree, we cut
off from consideration all the elements in the other branch. Compare
this with having to go through the whole list as we would with sets
represented by non-ordered lists if the element whose membership we
were testing were not in the list. Or having to go on average through
half the list if the set were represented by an order list. With the
tree representation, each time we go to one branch of the tree, we cut
all the elements from the other branch out of consideration without
looking at them, because we know the element we are looking for cannot
be found amongst them.
If our tree were perfectly balanced, meaning at any point in the tree there are exactly as many elements in the right subtree as in the left, each time we move to the right or left, we would cut the number of elements we are considering by half. This is similar to the way binary search of an array works.
However, we have no guarantee that our trees will be perfectly balanced. There are many different ordered trees that store the same set of numbers, and the shape a tree will become as it is constructed will depend on the order in which the numbers added to it are given. Consider, for example:
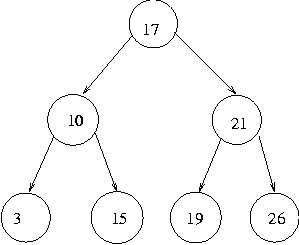
which is a perfectly balanced tree representing the set {3,10,15,17,19,21,26} and the tree:
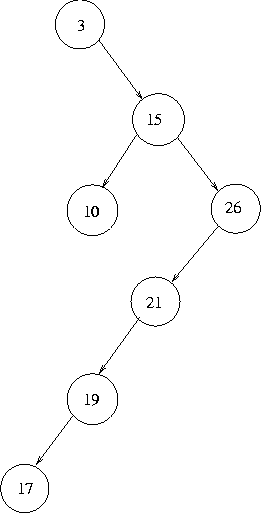
which represents the same set but is unbalanced. In the first case, to test whether an element is a member of the set, we would at most have to make three comparisons, whereas in the second case we might have to make up to six (to test if 16, 17 or 18 is in the set).
There are more complicated ways of adding integers to trees which ensure the trees remain balanced. These are used to avoid the problem of trees becoming unbalanced, which loses the advantage of using the tree structure. However, we will not discuss keeping trees balanced at this point.
Let us first consider how we would delete a number which is in what is known as a "leaf" of the tree, that is a cell which has no descendants. In this case, if we consider it just in terms of diagrams, it is obvious what we need to do. For example, to remove the number 7 from the tree below:
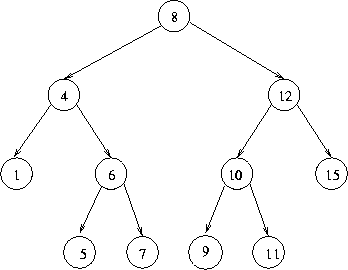
we obviously need to transform the tree to:
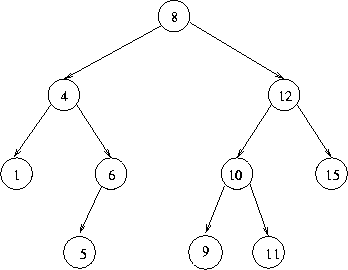
and something similar needs to be done if 1, 5, 9, 11 or 15 are removed.
To remove a leaf cell like this, we need to move a pointer to the cell above it in the tree:
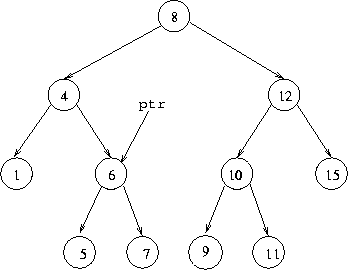
Now from this position, ptr.right=null will remove the
cell containing 7, while ptr.left=null will remove the
cell containing 5. It is necessary to do this from the cell above
because that causes the change through this cell being shared. You
might think that from the situation in the diagram above, executing
ptr=null would remove 5, 6 and 7 from the tree, but in
fact it makes no change to the tree. It sets ptr to
null, but this has no effect on the right
field of the cell containing 4.
Here is a code fragment which does the work of moving a pointer
ptr down the branches of a tree to find the number
n:
Cell ptr=tree;
while(ptr!=null&&ptr.item!=n)
if(n<ptr.item)
{
if(ptr.left!=null&&ptr.left.item==n&&
ptr.left.left==null&&ptr.left.right==null)
ptr.left=null;
ptr=ptr.left;
}
else if(n>ptr.item)
{
if(ptr.right!=null&&ptr.right.item==n&&
ptr.right.left==null&&ptr.right.right==null)
ptr.right=null;
ptr=ptr.right;
}
With this code, if the number n is found in a leaf
cell descending from the cell which ptr is referencing,
that leaf cell is deleted. The lines
if(ptr.right!=null&&ptr.right.item==n&&
ptr.right.left==null&&ptr.right.right==null)
ptr.right=null;
do this to delete a leaf to the right, as in the case of the number 7
in the example above. After this, executing ptr=ptr.left
sets ptr to null. Also, ptr
eventually becomes null if the number n
doesn't exist in the tree.
The difficult case comes when the number we want to delete isn't in
a leaf of the tree. In this case, the code above will leave
ptr pointing to the cell containing the number we wish
to delete. For example, in the case above if we wish to delete 12,
the code will leave us in this situation:
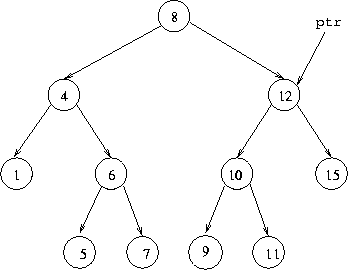
But we can't just remove 12 and leave a "hole" in the tree.
The situation is not too difficult to deal with if it happens that
one of the branches of the cell whose number we're deleting is
null, for example if we had:
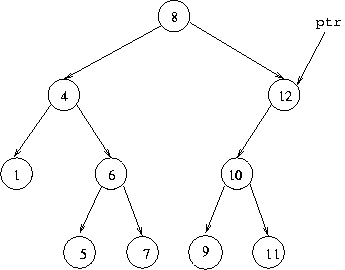
we would change the situation to:
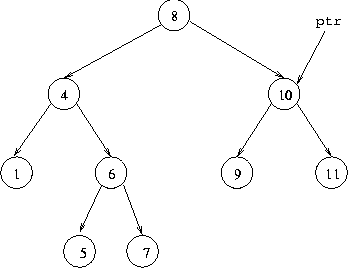
We can do this by actually copying the number 10 from ptr.left.item
into ptr.item, and similarly the links from ptr.left.left
and ptr.left.right into ptr.left and ptr.right.
When doing this, we must change the field ptr.left last
as changing it changes what ptr.left.right and
ptr.left.item mean. So this is done by the code:
ptr.item=ptr.left.item; ptr.left=ptr.left.left; ptr.right=ptr.left.right;
We could do something similar if the left subtree of the cell ptr
is referring to is null. But if neither the left nor the right
subtree is null we are in a more complicared position.
The highest number in the left subtree must be the number found by going to the left subtree and then following down all the right subtree links. We send a second pointer down to the cell that points to the rightmost cell. For example, with the following situation:
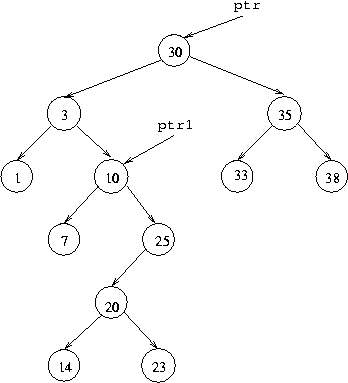
the number 25 is the biggest in the left subtree, so to delete the
number 30, we replace it by 25, and delete the cell containing 25.
The diagram above shows the final position of the second pointer,
called ptr1 to do this deletion. The position we want
to end up with is:
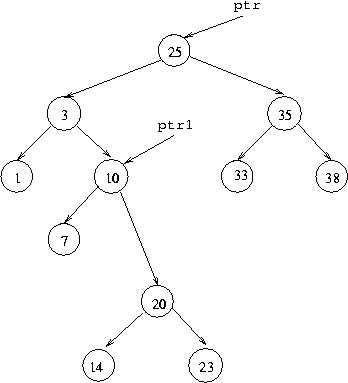
The following code will do this:
ptr.item=ptr1.right.item; ptr1.right=ptr1.right.left;
Putting together all the code necessary to delete an integer from an
ordered tree of integers gives us the following code for the method
delete:
public void delete(int n)
{
Cell ptr=tree;
while(ptr!=null&&ptr.item!=n)
if(n<ptr.item)
{
if(ptr.left!=null&&ptr.left.item==n&&
ptr.left.left==null&&ptr.left.right==null)
ptr.left=null;
ptr=ptr.left;
}
else if(n>ptr.item)
{
if(ptr.right!=null&&ptr.right.item==n&&
ptr.right.left==null&&ptr.right.right==null)
ptr.right=null;
ptr=ptr.right;
}
if(ptr!=null)
if(ptr.left==null)
{
ptr.item=ptr.right.item;
ptr.left=ptr.right.left;
ptr.right=ptr.right.right;
}
else if(ptr.right==null)
{
ptr.item=ptr.left.item;
ptr.right=ptr.left.right;
ptr.left=ptr.left.left;
}
else if(ptr.left.right==null)
{
ptr.item=ptr.left.item;
ptr.left=ptr.left.left;
}
else
{
Cell ptr1=ptr.left;
while(ptr1.right.right!=null)
ptr1=ptr1.right;
ptr.item=ptr1.right.item;
ptr1.right=ptr1.right.left;
}
}
public String toString()
{
return numbersIn(tree);
}
private static String numbersIn(Cell tree)
{
if(tree==null)
return "";
else
return numbersIn(tree.left)+" "+tree.item+" "+numbersIn(tree.right);
}
Note that the numbers will be given in ascending order. This is because
we give the node value number in between the numbers in the left
subtree and the numbers in the right subtree, and we know it must come
in between numerically. But the same applies to the left subtree and
right subtree. So putting numbers into an ordered search tree, and then
flattening the tree into a list of numbers can be a way of sorting those
numbers.
In the above code, there is a public method which makes use of an
auxiliary private method. The public method is non-static, and when
it refers to tree it means the tree field
of the object the call to the method is attached to. But the private
method takes the tree it is flattening as its parameter, rather than
from an object it is attached to. Therefore it can be declared as
static.
The actual code we use for giving a correct representation of sets has to
be a little more sophisticated than the above. It needs to put braces
round the numbers, and commas in the correct places between the numbers.
So here's the code:
public String toString()
{
return "{"+toString(tree)+"}";
}
private static String toString(Cell tree)
{
if(tree==null)
return "";
else if(tree.left==null&&tree.right==null)
return ""+tree.item;
else if(tree.left==null)
return tree.item+","+toString(tree.right);
else if(tree.right==null)
return toString(tree.left)+","+tree.item;
else
return toString(tree.left)+","+tree.item+","+toString(tree.right);
}
t which prints a representation of the
tree which stores the current set. It's fairly crude, as it would be
a much more difficult problem to print a representation in the
form with the root at the top. In this case, the root is at the
left side, and there are no lines drawn between the numbers.
import java.io.*;
class UseIntSets12
{
// Set maintenance program
// Uses set class IntSet13
public static void main(String[] args)
throws IOException
{
int n=0;
char ch;
String line;
BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
IntSet13 mySet = new IntSet13();
do {
System.out.print(": ");
line = in.readLine();
ch = line.charAt(0);
if(line.length()>1)
n = Integer.parseInt(line.substring(1).trim());
switch(ch)
{
case 'q' :
break;
case 'd' :
mySet.delete(n);
break;
case 'a' :
mySet.add(n);
break;
case 'm' :
if(mySet.member(n))
System.out.println("Is a member");
else
System.out.println("Not a member");
break;
case 'p':
System.out.println(mySet);
break;
case 't':
System.out.println(mySet.treeString());
break;
default:
System.out.print("d - delete, a - add, m - member,");
System.out.println(" p - print, t - tree print, q - quit");
break;
}
}
while(ch!='q');
}
}
class IntSet13
{
// Destructive Set class, sets stored as ordered trees
Cell tree;
public void delete(int n)
{
Cell ptr=tree;
while(ptr!=null&&ptr.item!=n)
if(n<ptr.item)
{
if(ptr.left!=null&&ptr.left.item==n&&
ptr.left.left==null&&ptr.left.right==null)
ptr.left=null;
ptr=ptr.left;
}
else if(n>ptr.item)
{
if(ptr.right!=null&&ptr.right.item==n&&
ptr.right.left==null&&ptr.right.right==null)
ptr.right=null;
ptr=ptr.right;
}
if(ptr!=null)
if(ptr.left==null)
{
ptr.item=ptr.right.item;
ptr.left=ptr.right.left;
ptr.right=ptr.right.right;
}
else if(ptr.right==null)
{
ptr.item=ptr.left.item;
ptr.right=ptr.left.right;
ptr.left=ptr.left.left;
}
else if(ptr.left.right==null)
{
ptr.item=ptr.left.item;
ptr.left=ptr.left.left;
}
else
{
Cell ptr1=ptr.left;
while(ptr1.right.right!=null)
ptr1=ptr1.right;
ptr.item=ptr1.right.item;
ptr1.right=ptr1.right.left;
}
}
public void add(int n)
{
if(tree==null)
tree = new Cell(n,null,null);
else
{
Cell ptr=tree;
while(ptr.item!=n)
if(n<ptr.item)
{
if(ptr.left==null)
ptr.left = new Cell(n,null,null);
ptr = ptr.left;
}
else if(n>ptr.item)
{
if(ptr.right==null)
ptr.right = new Cell(n,null,null);
ptr = ptr.right;
}
}
}
public boolean member(int n)
{
Cell ptr=tree;
while(ptr!=null&&ptr.item!=n)
if(n<ptr.item)
ptr=ptr.left;
else
ptr=ptr.right;
return ptr!=null;
}
public String toString()
{
return "{"+toString(tree)+"}";
}
private static String toString(Cell tree)
{
if(tree==null)
return "";
else if(tree.left==null&&tree.right==null)
return ""+tree.item;
else if(tree.left==null)
return tree.item+","+toString(tree.right);
else if(tree.right==null)
return toString(tree.left)+","+tree.item;
else
return toString(tree.left)+","+tree.item+","+toString(tree.right);
}
public String treeString()
{
return treeString("",tree);
}
private String treeString(String indent,Cell tree)
{
if(tree==null)
return "\n";
else if(tree.left==null&&tree.right==null)
return indent+tree.item+"\n";
else
return treeString(indent+" ",tree.right)+
indent+tree.item+"\n"+
treeString(indent+" ",tree.left);
}
private static class Cell
{
int item;
Cell left,right;
Cell(int n,Cell l,Cell r)
{
item=n;
left=l;
right=r;
}
}
}
Last modified: 18 March 2002