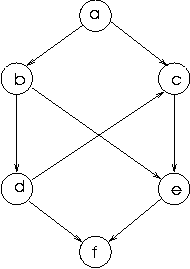

there is a path from node a to d which consists of the edge a-b followed by the edge b-d. But there is no path from d to a because we cannot follow edges in reverse, and there is no other combinatiom of edges that leads from d to a. We can express a path as an orderd list of nodes that forms the path, so the path from a to d can be expressed as [a,b,d].
A naïve algorithm to find a path from one node to another
starts at the initial node, finds a node that joins to the initial node,
then finds a node which joins to that node and so on until it reached the
final node. Here is a program that implements this algorithm:
import java.io.*;
import java.util.*;
class UseGraphs1
{
// Attempts to find shortest path with no backtracking
// Uses iteration
public static void main(String[] args)
throws IOException
{
BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
BufferedReader file;
System.out.print("Enter name of file for graph: ");
file = new BufferedReader(new FileReader(in.readLine().trim()));
Graph1 graph = new Graph1(file);
file.close();
System.out.print("Enter start node: ");
String start = in.readLine().trim();
System.out.print("Enter finish node: ");
String finish = in.readLine().trim();
String p = path(start,finish,graph);
System.out.println("Path is: ");
System.out.println(p);
}
public static String path(String start,String finish,Graph1 graph)
{
Cell p = findPath(start,finish,graph);
if(p==null)
return "No path found";
else
{
String str = p.first;
p = p.next;
while(p!=null)
{
str=p.first+","+str;
p=p.next;
}
return "["+str+"]";
}
}
private static Cell findPath(String start,String finish,Graph1 graph)
{
Cell done = new Cell(start,null);
Enumeration enum = graph.getLinks(start);
while(!done.first.equals(finish)&&enum.hasMoreElements())
{
String next = (String)enum.nextElement();
done = new Cell(next,done);
enum = graph.getLinks(next);
}
if(done.first.equals(finish))
return done;
else
return null;
}
private static class Cell
{
String first;
Cell next;
Cell(String f,Cell n)
{
first=f;
next=n;
}
}
}
You can see this class maintains its own nested class Cell
which is used to build a linked list of nodes representing the path.
The method path calls findPath to return
the linked list representing the path from the start to finish node
given as its first two arguments in the graph given as its third arguments.
It then converts this to a string representation which is returned.
Note that the linked list gives the nodes in reverse order as new nodes
are added to the front of the list referred to by done.
The order is reversed to the correct order in converting to the string
representation.
The representation of graphs is as given
previously, with the only public method being getLinks
which when given a node gives an Enumeration which
gives all the nodes wth edges it connects to by repeated calls of
getNextElement on it.
Suppose the file graph1 contains the text:
a b c b d e c e d c f e f fthen running the programe and entering
graph1 in
response to the prompt for a file and a and
e respectively in response to the prompt for
a start and finish mode causes [a,b,d,c,e] to be
printed.
As you can see, this is a path from a to e in the graph, but not the shortest path, which is either [a,b,e] or [a,c,e]. What happens is that at each node the algorithm takes the next node form the list of nodes and works from there, so at a it is d and so on.
Now suppose the graph were written in the file as:
a b c b d e c e d f c e f fAlthough we have previously written the connecting nodes in alphabetical order, we gave no requirement that they be written this way. The
Enumeration given by getLink follows the order
the order in the file, so now when we are at d
we move next to node f. But there are no outgoing
edges from node f. We are stuck there and can go
no further. This is represented in the code by findPath returning
null rather than the list of nodes visited, and
path returns a string giving an error message in this case.
If there are no outgoing edges from a node, the enumeration obtained
by giving that node as the argument to getLinks will
return false on the first call of hasMoreElements
on it, and nextElement can never be called on it without
causing an exception. That is why the loop in findPath has
two conditions joined by &&:
while(!done.first.equals(finish)&&enum.hasMoreElements())the first is a test that the path so far has not reached the node named by
finish, and the second a test that there
are some outgoing edges.
We shall ignore the problem of reaching dead-ends for the moment, and
in order to develop our path-finding algorithm consider representing
it recursively rather than iteratively. We saw
previously how iteration
could be converted to tail recursion. The rest of the program is the
same as above, but the methods
path and findPath becomes:
public static String path(String start,String finish,Graph1 graph)
{
Cell p = findPath(finish,graph,new Cell(start,null));
if(p==null)
return "No path found";
else
{
String str = p.first;
p = p.next;
while(p!=null)
{
str=p.first+","+str;
p=p.next;
}
return "["+str+"]";
}
}
private static Cell findPath(String finish,Graph1 graph,Cell done)
{
if(done.first.equals(finish))
return done;
else
{
Enumeration enum = graph.getLinks(done.first);
if(enum.hasMoreElements())
{
String next = (String)enum.nextElement();
return findPath(finish,graph,new Cell(next,done));
}
else
return null;
}
}
A slight change is that findPath now takes a linked
list representing a path as one of its arguments, initially
consisting of just the start node. When findPath is
called, the latest next node is the first node in
the list done.
We can think of this as declaring that a path in the graph referenced by
graph which builds on the path referenced by done
and leads to the node referenced by finish is either
done itself in the case where the first node in the path
is equal to finish, or is the path in graph
which leads to finish and builds on the path obtained by
adding to done the node at the other end of the first edge
that links from it. Or we return null if there are
no edges leading from the first node in the path referenced by
done. However we think of it, it is a translation of
the iterative code to recursion which does not change the algorithms, so
it will not behave any differently: it will still cause us to get stuck in
"dead-ends".
findPath which doesn't
get stuck in dead-ends:
private static Cell findPath(String finish,Graph1 graph,Cell done)
{
if(done.first.equals(finish))
return done;
else
{
Cell p=null;
Enumeration enum = graph.getLinks(done.first);
while(p==null&&enum.hasMoreElements())
{
String next = (String)enum.nextElement();
p=findPath(finish,graph,new Cell(next,done));
}
return p;
}
}
As before, it works by adding the first linking node to the list
of nodes encountered so far and then calling the findPath
method recursively to add on further nodes. But if the recursive call
returns null, instead of returning null
itself it tries adding the second linking node to the list of nodes
and calling findPath recursively using that as its base.
It goes through all the linking nodes until either the recursive call
does not return null or there are no linking nodes left,
and only if there are no linking nodes let to try does it return
null.
To consider in more detail how this code works, let us consider the
following graph:
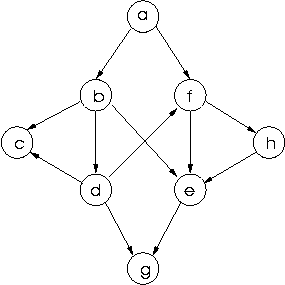
a b f b c d e c d c f g e g f e h g h eNodes c and g are dead-ends here, nodes without any edges leading from them.
If we wish to find a path from a to
h we start with the situation where
done represents the list [a]
which is represented by the cells-and-pointers structure:
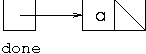
We create an enumeration giving the links from node
a. The first call of nextElement
on this enumeration returns b, so we make a
recursive call with done in the recursive call representing the
path [a,b], which is represented by the cells and
pointers structure:
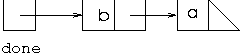
(note the cells and pointers structure stores the path in reverse order).
We then create an enumeration giving the links from node
b. The first call of nextElement
on this enumeration returns c. In the recursive
call made from here done represents the path
[a,b,c] represented by the cells and pointers structure:
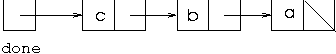
and an enumeration is created o give all the nodes leading from node c. The situation at this point could be illustrated using the environment diagrams we used previously to explain recursion:
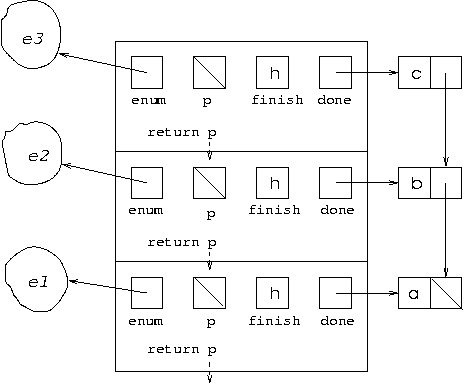
At this point, the call of hasMoreElements on
the enumeration e3 returns false
which causes the topmost recursive call to terminate returning
null. This now returns control to the recursive call
below it, which is in the loop and finds that its p
is still null but its enumeration,
e2, returns true when
hasMoreElements is called on it. So it gets the next node
from the enumeration, which is d, and makes a
further recursive call, this time with done representing
the path [a,b,d]. This call first checks that
the first element of its done, which is d,
is not equal to its finish which is h,
and finding it is not creates an enumeration to give the nodes leading
from d in the graph. This means our environment
diagram now looks like:
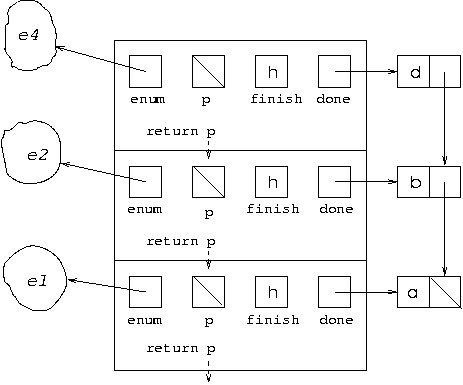
In effect, we have move back from the dead-end of node c to node b and tried the next edge leading from b which takes us to d.
As it happens, the first edge we will try from node d takes us to c again. This time we move back to d and try the next edge leading from it which takes us to f. So we have the situation where we have followed the path [a,b,d,f].
At this point we humans can see that if only we went to node
h next, we would have found a path. But our
algorithm will try the edges in the strict order they were given in the
file. So the edge leading to e is tried next,
giving us the path [a,b,d,f,e]. There is only
one edge leading from this taking us to g,
so we make a recursive call whose done argument represents
[a,b,d,f,e,g].
However, g is not the finish we
want, but it is a dead-end. We return null to the
call whose done represents [a,b,d,f,e].
But here there are no more edges leading out, so its enumeration returns
false when hasMoreElements is called on it.
So this call too returns null and we return to the call
representing the path [a,b,d,f].
Back at the call representing [a,b,d,f] we
now try the next edge leading from f and this
takes us to h. Our final recursive call
has its
What is happening here is known as
backtracking.
We have a problem that could return a solution, but could also return
a special value, in this case
We can think of this as a tree which is traversed
traversed preorder left-to-right,
until either a node is found which represents a solution, or all nodes
have been considered and no solution found.
In our path example, the nodes of the tree represent paths through the
graph being considered. The children of any node represent the paths
that can be obtained by adding one extra edge to the path of the the node.
For our graph above the
complete tree is:
Finding the path in this way is a
search problem.
We have a "space" of possible solutions, as described by the tree, and
we can consider solving the problem as searching through this tree to find
a node in it which is a solution, in this case where nodes represent
possible paths starting with our start node, a solution node is one whose
path ends with our finish node. Note, however, that the tree is
implicit in the algorithm, we do not construct a
tree data structure.
The search given by our program is known as
depth first search because it goes as deep as it can in the first
branch of the tree it is searching, backtracking and looking at other
branches only if no solution can be found in it.
If we looked for a path from node a to
f in the above
graph our search would start with a, then move to
the node representing the path [a,b] then to
the node representing [a,b,d], then to
[a,b,d,c], then to [a,b,d,c,b].
This represents a path which leads back onto itself, since now we
are back at the node b, and we follow the
same nodes as before, going to [a,b,d,c,b,d],
then to [a,b,d,c,b,d,c], then to
[a,b,d,c,b,d,c,b] and so on forever without
ever getting to a path which ends in f.
One way of thinking of this is that we are searching an infinite tree:
Last modified: 12th November 2001
done argument represent the path
[a,b,d,f,h]. Now the field done.first
is equal to finish, so this value of done is
returned as the result of the recursive call. This sets p
in the recursive call below it to something other than null
so it exits the loop and returns the same value, which has the same effect
on the recursive call below it, and so on down to the original call.
So [a,b,d,f,h] is returned as this algorithm's
answer to the request for a path from a
to h.
null indicating "no solution
found". We do not know which of several possible calls we should make
to find a solution, in this case which edge to add to the path
in making the recursive call. So we try all possibilities in turn until we
find one which returns us a solution rather than "no solution found".
Each time we get to a dead-end, that is a call which does not
represent a solution and has no calls at all that can be made from it,
we backtrack, that is go back to the last call we made where there
are alternative calls that can be tried, and try the next alternative.
a
/ \
/ \
/ \
/ \
/ \
/ \
/ \
/ \
ab af
/|\ / \
/ | \ / \
/ | \ | |
/ | \ | |
/ | \ | |
/ | \ | |
abc abd abe afe afh
/ | \ \ | |
/ | \ \ | |
/ | \ \ | |
abdc abdf abdg abeg afeg afhe
/ \ |
/ \ |
/ \ |
abdfe abdfh afheg
| |
| |
| |
abdfeg abdfhe
|
|
|
abdfheg
However, our attempt to find a path from a to
h only traverses the following part of the
tree:
a
/
/
/
/
/
/
/
/
ab
/|
/ |
/ |
/ |
/ |
/ |
abc abd
/ |
/ |
/ |
abdc abdf
/ \
/ \
/ \
abdfe abdfh
|
|
|
abdfeg
The rightmost leaf in this portion of the tree, labelled
abdfh represents a solution, the other leaves
represents dead-ends from which backtracking is necessary.
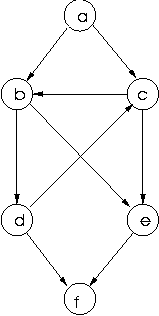
Cycles
Suppose we try our program above with the following graph:
a
/ \
/ \
/ \
/ \
/ \
/ \
/ \
ab ac
/\ /\
/ \ / \
/ \ / \
/ \ / \
abd abe acb ace
/ \ | / \ \
/ \ | / \ \
/ \ | / \ \
abdc abdf abef acbd acbe acef
/ \ /\ \
/ \ / \ \
/ \ / \ \
abdcb abdce acbdc acbdf acbef
/ \ | / \
/ ... | / ...
/ | /
infinite abdcef infinite
A depth-first left-to-right search will get caught in the infinite
branch and never get to solutions to its right.
private static Cell findPath(String finish,Graph1 graph,Cell done)
{
if(done.first.equals(finish))
return done;
else
{
Cell p=null;
Enumeration enum = graph.getLinks(done.first);
while(p==null&&enum.hasMoreElements())
{
String next = (String)enum.nextElement();
if(!member(next,done))
p=findPath(finish,graph,new Cell(next,done));
}
return p;
}
}
with need for a new private method, which could be expressed
recursively:
private static boolean member(String node,Cell list)
{
if(list==null)
return false;
else if(list.first.equals(node))
return true;
else
return member(node,list.next);
}
or iteratively:
private static boolean member(String node,Cell list)
{
Cell ptr;
for(ptr=list; ptr!=null&&!ptr.first.equals(node); ptr=ptr.next);
return ptr!=null;
}
The iterative version would be more efficient since it does not
involve the overhead of method calling, but the difference of efficiency
would be a constant factor, not an order of magnitude, since both are
essentially the same algorithm differently expressed.
Matthew Huntbach