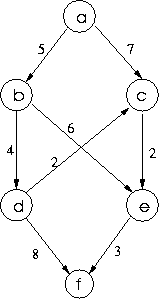
Although this graph is directed, costed graphs are often undirected.
Here, for example, is a costed directed graph represented diagrammatically:

The file representation could be similar to before, with each line in the graph containing a node followed by the list of nodes to which it has an edge connecting, but this time with a number following the destination node giving the cost of the edge. So the following:
a b 5 c 7 b d 4 e 6 c e 2 d c 2 f 8 e f 3 frepresents the graph above.
We could use a similar data structure to that used before, except that this time the nodes representing edges must have an extra field to store the cost of each edge.
The enumeration which returns the edges connecting to a particular
node must return the cost as well. We do this by defining a simple class
called Arc, and the enumeration returns Arc objects.
Here is the class Arc:
class Arc
{
String from,to;
int cost;
Arc(String f,String t,int c)
{
from=f;
to=t;
cost=c;
}
String getFrom()
{
return from;
}
String getTo()
{
return to;
}
int getCost()
{
return cost;
}
}
As you can see, an Arc object stores both the source
and destination node as well as the cost, though in our examples the
source node won't be used.
Now here is a class for constructing a costed graph object from
a file representation, with the object as
before having just
one public method, one which returns an enumeration giving all
the edges (in the form of Arc objects) that link to a
particular node:
import java.io.*;
import java.util.*;
class CGraph1
{
private ACell adjList;
public CGraph1(BufferedReader file)
throws IOException
{
String line = file.readLine();
adjList=null;
while(!line.equals(""))
{
NCell nlist,ptr=null;
StringTokenizer toks = new StringTokenizer(line);
String first = toks.nextToken();
if(toks.hasMoreTokens())
{
String node = toks.nextToken();
int cost = Integer.parseInt(toks.nextToken());
nlist = new NCell(node,cost);
ptr=nlist;
}
else
nlist=null;
while(toks.hasMoreTokens())
{
String node = toks.nextToken();
int cost = Integer.parseInt(toks.nextToken());
ptr.next = new NCell(node,cost);
ptr = ptr.next;
}
adjList = new ACell(first,nlist,adjList);
line = file.readLine();
}
}
public Enumeration getLinks(String from)
{
return new NextNodes(from);
}
private static class NCell
{
String first;
int cost;
NCell next;
NCell(String n,int c)
{
first=n;
cost=c;
next=null;
}
}
private static class ACell
{
String from;
NCell to;
ACell next;
ACell(String f,NCell t,ACell n)
{
from=f;
to=t;
next=n;
}
}
private class NextNodes implements Enumeration
{
NCell nlist;
String from;
NextNodes(String f)
{
from=f;
ACell ptr = adjList;
for(;ptr!=null&&!ptr.from.equals(from); ptr=ptr.next);
if(ptr==null)
nlist=null;
else
nlist=ptr.to;
}
public boolean hasMoreElements()
{
return nlist!=null;
}
public Object nextElement()
{
String to=nlist.first;
int c=nlist.cost;
nlist=nlist.next;
return new Arc(from,to,c);
}
}
}
Note that the cheapest path between two nodes may not be the shortest in terms of the number of edges, though it is the above graph. A path may be longer than another between the same nodes, but cheaper. For example, the path [a,b,d,c,e,f] in the above costed graph is longer than the path [a,b,d,f] between the same nodes, but cheaper at a cost of 16 as opposed to 17. As a result, we cannot expect breadth-first search to give us the cheapest path as its first path when used for costed graphs.
Below is a program which uses the branch-and-bound algorithm discussed
previously to find the
cheapest path between two nodes in a costed graph. This uses a static
variable called best to hold the cheapest path found so far
in a left-to-right depth-first search. If the cost of the path at any
place in the search tree is not less than the cost of the cheapest path
found so far, no search is done of any paths that extend it, because
(assuming there is no such thing as edges with negative costs) none of
them can be a cheaper path.
import java.io.*;
import java.util.*;
class UseCGraphs3
{
// Costed path search, depth-first, search all paths for shortest
// Uses branch-and-bound
private static int count;
private static Path best;
public static void main(String[] args)
throws IOException
{
BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
BufferedReader file;
System.out.print("Enter name of file for graph: ");
file = new BufferedReader(new FileReader(in.readLine().trim()));
CGraph1 graph = new CGraph1(file);
file.close();
System.out.print("Enter start node: ");
String start = in.readLine().trim();
System.out.print("Enter finish node: ");
String finish = in.readLine().trim();
count=0;
String p = path(start,finish,graph);
System.out.println("Path (after considering "+count+" paths) is: ");
System.out.println(p);
}
public static String path(String start,String finish,CGraph1 graph)
{
best=null;
findPath(finish,graph,new Path(new Cell(start,null),0));
if(best==null)
return "No path possible";
else
{
Cell p = best.getRoute();
String str = p.first;
p = p.next;
while(p!=null)
{
str=p.first+", "+str;
p=p.next;
}
return "Cost: "+best.getCost()+" Route: "+str;
}
}
private static void findPath(String finish,CGraph1 graph,Path done)
{
count++;
if(done.getRoute().first.equals(finish))
{
if(best==null||done.getCost()<best.getCost())
best=done;
}
else
{
Enumeration enum = graph.getLinks(done.getRoute().first);
while(enum.hasMoreElements())
{
Arc next = (Arc)enum.nextElement();
if(!member(next.getTo(),done.getRoute()))
{
Path branch = addArc(next,done);
if(best==null||branch.getCost()<best.getCost())
findPath(finish,graph,addArc(next,done));
}
}
}
}
private static Path addArc(Arc arc,Path p)
{
Cell r = new Cell(arc.getTo(),p.getRoute());
int c = arc.getCost()+p.getCost();
return new Path(r,c);
}
private static boolean member(String node,Cell list)
{
Cell ptr;
for(ptr=list; ptr!=null&&!ptr.first.equals(node); ptr=ptr.next);
return ptr!=null;
}
private static class Cell
{
String first;
Cell next;
Cell(String f,Cell n)
{
first=f;
next=n;
}
}
private static class Path
{
Cell route;
int cost;
Path(Cell r,int c)
{
route=r;
cost=c;
}
int getCost()
{
return cost;
}
Cell getRoute()
{
return route;
}
}
}
Note there is a separate nested class Path which stores
a linked list of Cell objects representing a path,
together with the cost of that path. So path costs are stored as part
of the object representing a path and do not need to be recalculated
every time we compare two paths to see which is the shortest.
If we consider the following graph:
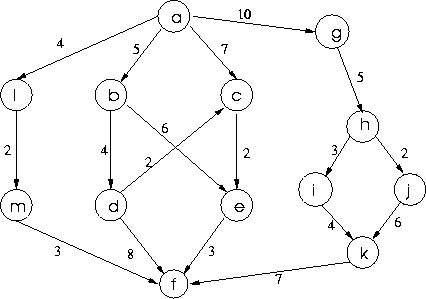
a b 5 c 7 g 10 l 4 b d 4 e 6 c e 2 d c 2 f 8 e f 3 f g h 5 h i 3 j 2 i k 4 j k 6 k f 7 l m 2 m f 3depth-first search will ensure the paths are considered in alphabetic order. So [a,c,e,f] with cost 12 will be considered before [a,g] with cost 10. Suppose we are searching for a path from a to f. When the search reaches [a,g] the path [a,c,e,f] will be already have been found and kept as the cheapest path found so far. The cost of [a,g] is less, so search goes on to consider [a,g,h]. But as the cost of [a,g,h,i] is 15 which is greater than 12, so further search extending this path, which would involve consideration of [a,g,h,i], [a,g,h,i,k], [a,g,h,i,k,f], [a,g,h,j], [a,g,h,j,k] and [a,g,h,j,k,f], is not done. However, it is only after this that search goes on to consider [a,l] then [a,l,m] then [a,l,m,f] and finds a cheaper path from a to f, at a cost of 9. If this path had been found first, we needn't have bothered with some of the other search, for example once we got to [a,b,d] since this has a cost of 9, we would know we couldn't find the lowest cost path as an extension of it, so [a,b,d,c], [a,b,d,c,e], [a,b,d,c,e,f] and [a,b,d,f] would never have been considered.
In our graph above, searching for the cheapest path from a to f, this means we initialise the collection with [a] then take that out and add its descendants: [a,b] with cost 5, [a,c] with cost 7, [a,g] with cost 10 and [a,l] with cost 4. The cheapest of these is [a,l], so we take it out, find it does not lead to our finish node, so add its one descendant [a,l,m] with cost 6. Now [a,b] is cheapest, so we take it out and add its two descendants [a,b,d] with cost 9 and [a,b,e] with cost 11. After this, [a,l,m] is the cheapest path so we take it out and add its one descendant [a,l,m,f] with cost 9.
You might think we have now found the solution and can finish. But we don't check whether a path reaches to the finish node until we take it out of the collection. Suppose there were a path from c to f with cost 1. Then [a,c,f] with cost 8 would be the cheapest path from a to f, and we wouldn't produce that until we take out [a,c] next. But the one descendant of [a,c] is [a,c,e] of cost 9. Although this is the same cost as [a,l,m,f], if the rule is that when two paths have the same cost the one that was produced first is taken out, [a,l,m,f] will be taken out at this point and returned as a lowest cost solution.
To achieve best-first search, we need an object to store the collection of paths, similar to the way we have used queues and stacks to store collections of paths. In a queue, when an item is taken from the collection it will be the one remaining in the collection that has been there longest. In a stack, when an item is taken from the collection it will be the one in the collection that has been there shortest. But in the collection used here, when an item is removed from the collection, it must always be the lowest cost one. An abstract data type which behaves in this way is called a priority queue.
The methods for a priority queue here are almost exactly like those
we have already seen for Queues:
first to give the first item in the structure (without
removing it from the structure), leave to alter the
structure and remove its first item (without returning anything),
join to add a new item to the structure, and isEmpty
to test whether the structure is empty (signalled by the boolean
value returned). However, the items in the priority queue are given
as type Comparable rather than type
Object. The behaviour
is different because the order in which items are put into a priority
queue is not necessarily the order in which they appear as they are
taken out.
Comparable
is another built-in type in Java, defined by a simple
interface. The only method given
in the interface Comparable has signature:
public int compareTo(Object o)So any class that implements class
Comparable must have
a method with this signature, and you can see the nested class Path
in the code above
has it so that it can implement Comparable. As the
interface has nothing else in it, it defined a type which is general
except for this requirement.
The idea is that Comparable is a class of objects
with an ordering among themselves. You might think this could be
given by a method, say, lessThan as we saw with
KeyObject,
where if c1 and c2 are of type
Comparable, then c1.lessThan(c2) returns
true if c1 comes before c2
in the ordering, and false otherwise. However,
compareTo can deliver three possible values, indicating
whether two items are equal to each other in the ordering as well
as ordered either one way in the ordering or the other. So
c1.compareTo(c2) returns an int value, which
is 0 if the c1 and c2 are equal in the
ordering, a negative number if c1 comes before
c2 in the ordering and a positive number if
c1 comes before c2 in the ordering. The
actual number returned does not matter apart from it having to be 0,
positive or negative.
The ordering of Path objects is given by their costs,
which can be accessed directly inside the class Path
by referring to the field cost. Note that the signature
for compareTo in this class has to match that given in
the interface, so the argument to it is of type Object,
not of type Path (nor is it of type Comparable,
though that would make sense). So the argument has to be type cast into
type Path in the code for method compareTo in
class Path.
When items are put into a priority queue, they are compared to each
other using the ordering defined by their own compareTo
method. The method first when called on a priority queue
will always return an object c1 such that
c1.compareTo(c2) is negative or 0 for any item
c2 which has been added to the priority queue using
join but never deleted using leave.
A call of leave on a priority queue object will always
cause to be removed from the priority queue that item which immediately
before the call would have been returned if first has
been called on the priority queue object then.
We will leave discussion of the implementation of priority queues to another set of notes.
Last modified: 20th November 2001