Priority queues

A linked-list implementation of priority queues

In the form of priority queue we suggested, items in the structure had their own fixed ordering determined by them being of a class which is a subclass of the class defined by Java's built-in interface Comparable. Any class which implements Comparable must have a method compareTo within it, which defines an ordering for members of that class.

An obvious implementation of priority queues, based on what we have covered before, is to use a linked list structure, in which the items in the list are stored in the order given by their compareTo method. The first item in the list will always be the one which is removed when an item is taken from the collection, so that is simple to implement. Inserting an item in the list involves running down the list until its appropriate place is found, in the way we have already considered when adding items to ordered linked lists. Below is code for this implementation:

class PrioQueue1
{
// Priority Queue implemented using an ordered linked list

 Cell list;

 public Comparable first()
 {
  return list.first;
 }

 public void leave()
 {
  list=list.next;
 }

 public void join(Comparable obj)
 {
  if(list==null)
    list = new Cell(obj,null);
  else if(obj.compareTo(list.first)<0)
     list = new Cell(obj,list);
  else
     {
      Cell ptr;
      for(ptr=list; 
          ptr.next!=null&&ptr.next.first.compareTo(obj)<0; 
          ptr=ptr.next);
      ptr.next = new Cell(obj,ptr.next);
     }
 }

 public boolean isEmpty()
 {
  return list==null;
 }

 private static class Cell
 {
  Comparable first;
  Cell next;

  Cell(Comparable f,Cell n)
  {
   first=f;
   next=n;
  }
 }
}

Priority queues implemented as heaps

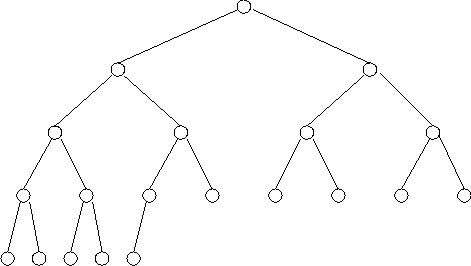
Whereas ordered binary trees could be unbalanced: any node could have one branch which is empty and the other not empty, binary trees with the heap property have to be complete. A complete binary tree of height h is full down to level h-2, that is all nodes have a non-empty left and right branch. At level h-1, when a node has a branch it must be the left branch, and all nodes to its left must have a left and a right branch, All nodes at level h have both left and right branches empty.

This explains it formally, but it is more intuitively demonstrated by a diagram:

This is a complete binary tree, the only way to add an item and keep it complete is to change it to:

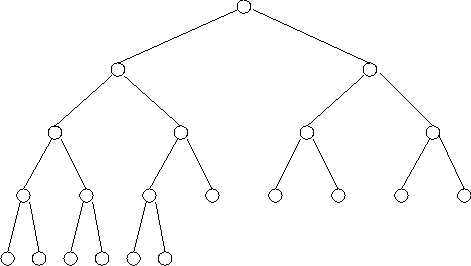
the only way to take an item and keep it complete is to change it to:

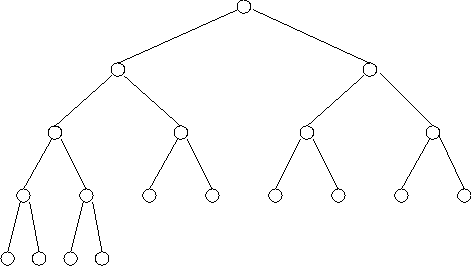
Heaps have the property that an item can be added or deleted from the structure keeping its heap property in O(log n) time, which is more efficient for adding an item than the O(n) time of an ordered linked list.

Now let us consider an example with numbers (as with sets, it is easy to show how data structures work when considering using them to store numbers, though in practice we would want to use them for more complex data items). The following shows a tree of integers which has the heap property:

Now if we add the number 5 to this tree as suggested above to keep the tree complete we get:

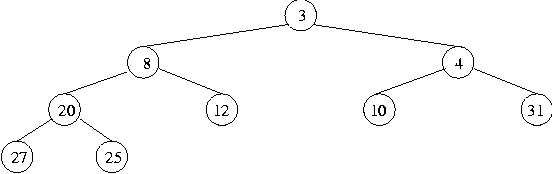
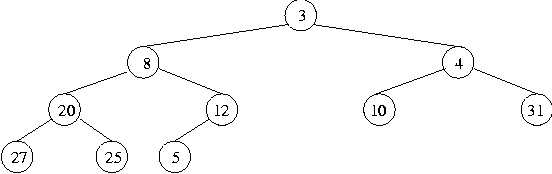
The number has to be added to the bottom row in order from the left (if the bottom row were full, it would be added as the first number on a new bottom row, taking the leftmost position). Although this tree is complete, it doesn't have the heap property, since in a heap all items have to be greater than the item in their parent node, but here the number 5 has a parent node with number 12. We resolve this by swapping those two out-of-order numbers, giving:

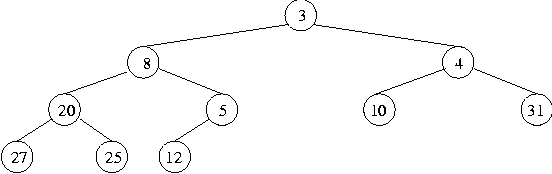
But this still doesn't have the heap property, since 5 is now below the greater number 8, so again we swap, giving:

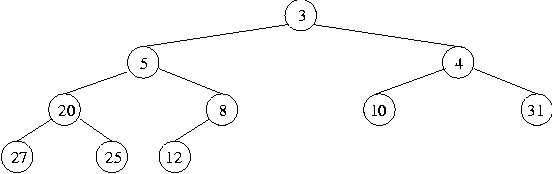
This does have the heap property. So this is how a number is inserted into a heap: firstly add the number in the position in the tree required to keep the tree complete; secondly, if the number is less than the number in its parent node in the tree, swap it with its parent and continue swapping until the number is not less than its parent, or it is in the root node of the whole tree.

Now suppose we want to delete the root node of the tree (and the only delete operation from a heap is to delete the root node). What is done is to replace the value of the root node by the value of the rightmost node in the last row of the tree, and then to delete that node. So if we wanted to continue from the above to delete the root node (storing 3, which by definition of a heap must be the smallest number in the heap), we get:

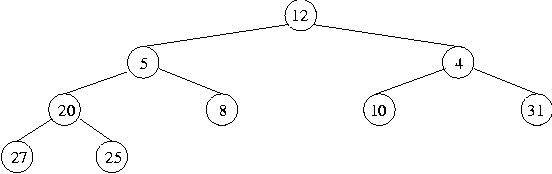
Again, this leaves the tree complete but without the heap property. The new root node value must be swapped with the smaller root of its two descendant branches (if it were swapped with the bigger, it would mean the bigger above the smaller). Performing this swap in this case gives:

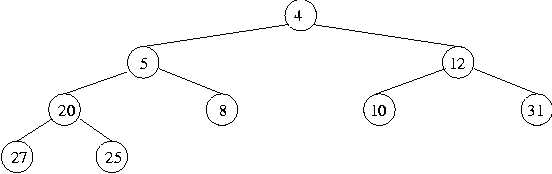
This does not have the heap property, since 12 is above the smaller value 10 in the tree, so it is swapped again, giving:

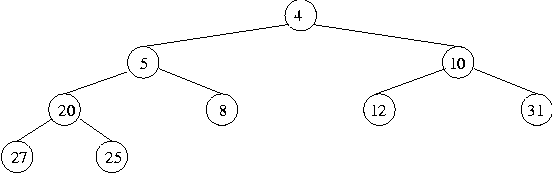
Now 12 is not above anything, since it is a leaf node, so the heap property holds. So, in general, to remove the smallest item from a heap, firstly replace the value in the root node with the value in the rightmost node of the lowest level and delete that node, secondly repeatedly swap the root node with its smaller descendant until it is in a position where it is either a leaf or its descendants are smaller.

Heaps implemented by arrays

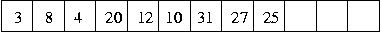
As you can see, the array is of a length longer than the number of items in the heap, so the structure needs to be represented as an array and count, that is with a separate int field saying how much of the array is currently being used for data. If a is the array and count is the count, then a[count] is the cell into which a new number should be put initially (and then count increased by 1), before sifting the number up in the tree as necessary to restore the heap property. When the lowest integer is taken from the heap, the integer in a[count-1] is copied into a[0], and then sifted down as required to restore the heap property.

So here is the position, showing the count, in the count and array representation after adding the number 5:

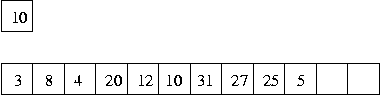
After the first swap of this new number, the situation is:

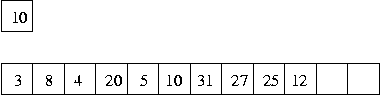
After the second swap, which returns the structure to a heap representation, the situation is:

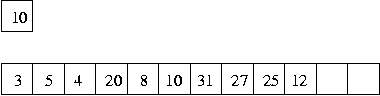
It is easy to work out which integers to swap in the array to restore the heap property: the parent node in the tree of the branch whose root is stored in a[i] is stored in a[(i-1)/2], while the roots of the two sub-branches of the branch whose node value is stored in a[i] are stored in a[i*2+1] and a[i*2+2].

With this, we can now give some code which implements the type IntHeap storing a heap of integers:

class IntHeap
{
 public static final int MAX = 127;
 private int count;
 private int[] array;
 

 public IntHeap()
 {
  array = new int[MAX];
  count=0;
 }

 public void delete()
 {
  array[0]=array[--count];
  siftDown(0);
 }

 public void add(int n)
 {
  array[count++]=n;
  siftUp(count-1);
 }

 public int first()
 {
  return array[0];
 }

 public String toString()
 {
  if(count==0)
    return "[]";
  else
     {
      String str="["+array[0];
      for(int i=1; i<count; i++)
         str+=","+array[i];
      return str+"]";
     }
 }

 public String treeString()
 {
  return treeString("",0);
 }

 private String treeString(String indent,int i)
 {
  int p=i*2;
  String str="";
  if(count>p+2)
     str+=treeString(indent+"     ",p+2);
  str+=indent+array[i]+'\n';
  if(count>p+1)
     str+=treeString(indent+"     ",p+1);
  return str;
 }

 private void siftUp(int i)
 {
  int p=(i-1)/2;
  while(i>0&&array[i]<array[p])
     {
      swap(i,p);
      i=p;
      p=(i-1)/2;
     }
 }

 private void siftDown(int i)
 {
  int d=i*2+1;
  while(count>d+1&&(array[i]>array[d]||array[i]>array[d+1]))
     {
      if(array[d]<array[d+1])
         {
          swap(i,d);
          i=d;
         }
      else 
         {
          swap(i,d+1);
          i=d+1;
         }
      d=i*2+1;
     }
  if(count==d+1)
     {
      if(array[i]>array[d])
          swap(i,d);
     }
 }

 private void swap(int i,int j)
 {
  int temp;
  temp = array[i];
  array[i] = array[j];
  array[j] = temp;
 }
}

Here is a simple front-end to enable heaps to be demonstrated:

import java.io.*;

class UseHeaps
{
// Heap maintenance 

 public static void main(String[] args)
 throws IOException
 {
  int n=0;
  char ch;
  String line;
  BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
  IntHeap myHeap = new IntHeap();
  do {
      System.out.print(": ");
      line = in.readLine();
      ch = line.charAt(0);
      if(line.length()>1)
         n = Integer.parseInt(line.substring(1).trim());
      switch(ch)
         {
          case 'q' : 
            break;
          case 'd' :
            myHeap.delete();
            break;
          case 'a' :
            myHeap.add(n);
            break;
          case 'f':
            System.out.println(myHeap.first());
            break;
          case 'p':
            System.out.println(myHeap);
            break;
          case 't':
            System.out.print(myHeap.treeString());
            break;
          default:
            System.out.print("d - delete, a - add, f - first,");
            System.out.println(" p - print, t - tree print, q - quit");
            break;
         }
     }
  while(ch!='q');
 }

}

We can adapt the code above to implement priority queues storing objects of class Comparable rather than integers. Rather than using < and > to compare the items in the structure, we need to use compareTo. Also we needn't include string representation methods. So this results in the code:

class PrioQueue2
{
// Priority Queue implemented using a heap

 public static final int MAX = 127;
 private int count;
 private Comparable[] array;
 

 public PrioQueue2()
 {
  array = new Comparable[MAX];
  count=0;
 }

 public void leave()
 {
  array[0]=array[--count];
  siftDown(0);
 }

 public void join(Comparable obj)
 {
  array[count++]=obj;
  siftUp(count-1);
 }

 public Comparable first()
 {
  return array[0];
 }

 public boolean isEmpty()
 {
  return (count==0);
 }

 private void siftUp(int i)
 {
  int p=(i-1)/2;
  while(i>0&&array[i].compareTo(array[p])<0)
     {
      swap(i,p);
      i=p;
      p=(i-1)/2;
     }
 }

 private void siftDown(int i)
 {
  int d=i*2+1;
  while(count>d+1&&
        (array[i].compareTo(array[d])>0||array[i].compareTo(array[d+1])>0))
     {
      if(array[d].compareTo(array[d+1])<0)
         {
          swap(i,d);
          i=d;
         }
      else 
         {
          swap(i,d+1);
          i=d+1;
         }
      d=i*2+1;
     }
  if(count==d+1)
     {
      if(array[i].compareTo(array[d])>0)
          swap(i,d);
     }
 }

 private void swap(int i,int j)
 {
  Comparable temp;
  temp = array[i];
  array[i] = array[j];
  array[j] = temp;
 }
}

Last modified: 7 May 2001