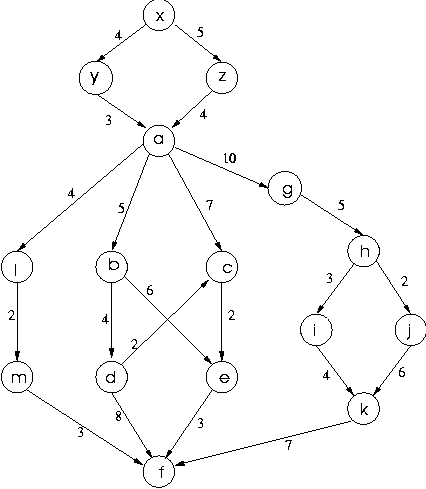

This is similar to the graph used for illustration previously, with just the addition of the three nodes x, y and z together with edges x-y, x-z, y-a and z-a.
Now, suppose we are searching for a path from x to a. All paths must go through node a, either via y or z. In fact the search tree for the path from x will look like:
x
/ \
/ \
/ \
xy xz
/ \
/ \
/ \
xya xza
/ \ / \
/...\ /...\
with the descendants of xya and
xza being identical except that the
former all start with xya and the
latter with xza. In fact there is no
need at all to search any of the tree with root xza,
since it cannot provide any path that is cheaper than the path which is
otherwise the same but goes through y rather
than z. All the paths going through
z will be 2 more expensive than the equivalent
going through y. Best-first search, for
example, will consider the path [x,z,a,b]
with cost 14 before it considers the path [x,y,a,l,m,f]
with cost 16 on a search for a path from x
to f even though it cannot possibly lead
to the cheapest solution.
Since once you have reached a the rest of your journey does not depend on how you got there, once we have done one search starting from there we needn't do any more. The same applies in general. So what is needed is a record in the search of nodes that have been reached. Once a node has been reached in one place in the search if it is reached later anywhere there is no further search following from it. This replaces the cycle check we considered previously, which only cut out search of a path which reached a node that had already been reached by one of its ancestors in the search tree.
The code below shows this. It keeps a set of strings representing the nodes visited. Each time a node is reached in the search, it is added to this set. Each time a new path is taken from the priority queue of paths (stored in cost order), if it leads to a node already in the set, it is not considered because that means a cheaper path to that node has already been found. Also a new path is not added if it leads to a node already in the set of visited nodes. Both tests are necessary because when a path is already in the priority queue, another path leading to the same node buit of a cheaper cost may be added. So when a path is added its destination node is not in the set of visited nodes, but it could be when it is taken out.
import java.io.*;
import java.util.*;
class UseCGraphs5
{
// Costed path search best-first, no node revisited
private static int count;
public static void main(String[] args)
throws IOException
{
BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
BufferedReader file;
System.out.print("Enter name of file for graph: ");
file = new BufferedReader(new FileReader(in.readLine().trim()));
CGraph1 graph = new CGraph1(file);
file.close();
Set visited = new Set();
System.out.print("Enter start node: ");
String start = in.readLine().trim();
System.out.print("Enter finish node: ");
String finish = in.readLine().trim();
count=0;
String p = path(start,finish,graph,visited);
System.out.println("Path (after considering "+count+" paths) is: ");
System.out.println(p);
}
public static String path(String start,String finish,CGraph1 graph,Set visited)
{
Path sol = findPath(start,finish,graph,visited);
Cell p = sol.getRoute();
if(p==null)
return "No path possible";
else
{
String str = p.first;
p = p.next;
while(p!=null)
{
str=p.first+", "+str;
p=p.next;
}
return "Cost: "+sol.getCost()+" Route: "+str;
}
}
private static Path findPath(String start,String finish,CGraph1 graph,Set visited)
{
PrioQueue1 pq = new PrioQueue1();
pq.join(new Path(new Cell(start,null),0));
while(!pq.isEmpty())
{
Path done = (Path)pq.first();
pq.leave();
count++;
if(done.getRoute().first.equals(finish))
return done;
else
{
Enumeration enum = graph.getLinks(done.getRoute().first);
if(!visited.member(done.getRoute().first))
{
visited.add(done.getRoute().first);
while(enum.hasMoreElements())
{
Arc next = (Arc)enum.nextElement();
if(!visited.member(next.getTo()))
pq.join(addArc(next,done));
}
}
}
}
return null;
}
private static Path addArc(Arc arc,Path p)
{
Cell r = new Cell(arc.getTo(),p.getRoute());
int c = arc.getCost()+p.getCost();
return new Path(r,c);
}
private static class Cell
{
String first;
Cell next;
Cell(String f,Cell n)
{
first=f;
next=n;
}
}
private static class Path implements Comparable
{
Cell route;
int cost;
Path(Cell r,int c)
{
route=r;
cost=c;
}
int getCost()
{
return cost;
}
Cell getRoute()
{
return route;
}
public int compareTo(Object obj)
{
Path p = (Path)obj;
if(cost==p.cost)
return 0;
else if(cost<p.cost)
return -1;
else
return 1;
}
}
}
The type Set here is just like the sets of integers
we have considered previously, except that it stores strings rather
than integers. It could, for example, be implemented using a
tree of strings, just like the implementation of a set of integers using a
tree of integers. The only difference is
that where we compared integers using > and
< we compare strings using compareTo.
With two strings, str1 and str2,
str1.compareTo(str2) is a negative integer if
str1 comes before str2 in alphabetic
ordering, a positive integer if it comes after, and 0 if the two
strings are equal. But since the type String implements
the type Comparable,
we can make our Set class more general and use it to store
object of any type that implement Comparable. Here is the
code for it:
class Set
{
// Destructive Set class, sets stored as ordered trees
Cell tree;
public void delete(Comparable n)
{
if(tree!=null)
if(tree.left==null&&tree.right==null)
{
if(tree.item.compareTo(n)==0)
tree=null;
}
else
delete(n,tree);
}
private static void delete(Comparable n,Cell t)
{
int flag = n.compareTo(t.item);
if(flag<0)
if(t.left.left==null&&t.left.right==null)
{
if(t.left.item.compareTo(n)==0)
t.left=null;
}
else
delete(n,t.left);
else if(flag>0)
if(t.right.left==null&&t.right.right==null)
{
if(t.right.item.compareTo(n)==0)
t.right=null;
}
else
delete(n,t.right);
else if(t.left==null)
{
t.item=t.right.item;
t.right=t.right.right;
}
else if(t.left.right==null)
{
t.item=t.left.item;
t.left=t.left.left;
}
else
t.item = removeRightmost(t.left);
}
private static Comparable removeRightmost(Cell t)
{
if(t.right.right==null)
{
Comparable rightmost = t.right.item;
t.right = t.right.left;
return rightmost;
}
else
return removeRightmost(t.right);
}
public void add(Comparable n)
{
if(tree==null)
tree = new Cell(n,null,null);
else
add(n,tree);
}
private static void add(Comparable n,Cell t)
{
if(n.compareTo(t.item)<0)
if(t.left==null)
t.left = new Cell(n,null,null);
else
add(n,t.left);
else
if(t.right==null)
t.right = new Cell(n,null,null);
else
add(n,t.right);
}
public boolean member(Comparable n)
{
return member(n,tree);
}
private static boolean member(Comparable n,Cell t)
{
if(t==null)
return false;
else
{
int flag = n.compareTo(t.item);
if(flag==0)
return true;
else if(flag<0)
return member(n,t.left);
else
return member(n,t.right);
}
}
public boolean isEmpty()
{
return tree==null;
}
private static class Cell
{
Comparable item;
Cell left,right;
Cell(Comparable n,Cell l,Cell r)
{
item=n;
left=l;
right=r;
}
}
}
Also, it is only necessary with each path to store the cost of the full path and the final node and next to final node. That is because when the path is added to the collection of paths we can recreate the full cheapest path from the path to the next to final node. This reformulation gives us a version of what is known as Dijkstra's algorithm after the computer scientists who discovered it, Edsger Dijkstra.
Here is code which is reformulated from our previous code, as suggested, giving the cheapest route from a given node to all other nodes in a costed directed graph:
import java.io.*;
import java.util.*;
class UseCGraphs6
{
// Finds shortest path from one node to all others
public static void main(String[] args)
throws IOException
{
BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
BufferedReader file;
System.out.print("Enter name of file for graph: ");
file = new BufferedReader(new FileReader(in.readLine().trim()));
CGraph1 graph = new CGraph1(file);
file.close();
ETable paths = new ETable5();
System.out.print("Enter start node: ");
String start = in.readLine().trim();
System.out.println();
findPaths(start,graph,paths);
Enumeration enum = paths.getEnumeration();
while(enum.hasMoreElements())
{
Path p = (Path)enum.nextElement();
System.out.print("Destination: "+p.to+" Cost: "+p.cost);
System.out.println(" Route: "+getRoute(p.pred,paths)+p.to);
}
}
private static void findPaths(String start,CGraph1 graph,ETable paths)
{
PrioQueue1 pq = new PrioQueue1();
pq.join(new Path(start,null,0));
while(!pq.isEmpty())
{
Path p1 = (Path)pq.first();
pq.leave();
if(paths.retrieve(p1.to)==null)
{
Enumeration enum = graph.getLinks(p1.to);
paths.add(p1);
while(enum.hasMoreElements())
{
Arc next = (Arc)enum.nextElement();
Path p2 = new Path(next.getTo(),p1.to,p1.cost+next.getCost());
pq.join(p2);
}
}
}
}
private static String getRoute(String to,ETable paths)
{
if(to==null)
return "";
else
{
Path p = (Path)paths.retrieve(to);
return getRoute(p.pred,paths)+to+",";
}
}
private static class Path extends KeyObject implements Comparable
{
int cost;
String to,pred;
Path(String t,String p,int c)
{
cost=c;
to=t;
pred=p;
}
public String getKey()
{
return to;
}
public int compareTo(Object obj)
{
Path p = (Path)obj;
if(cost==p.cost)
return 0;
else if(cost<p.cost)
return -1;
else
return 1;
}
}
}
Note the cheapest paths found are stored in a table, of the type
ETable which we defined
previously.
The new Path class stores only the cost of the
full path, the final node in the field to and the
next to final node in the field pred. As this is
a private nested class for use only within the enclosing
class, these fields can be accessed directly rather than through
methods. The class has to extend KeyObject so that
objects of its type can be put in tables of type ETable.
This requires implementing getKey() which returns the value
of the to field. The class is also stated as
implementing the Comparable interface, which is necessary
so that objects of its type can be put into priority queues of type
PrioQueue. We could declared KeyObject
as implementing the Comparable interface, as it has the
required, compareTo method, but we didn't. Note that
while a class can only extend one other class, it can
implement any number of interfaces.
The check for membership of the set of visited nodes is whether a path ending in the given node can be retrieved from the table of cheapest paths. In this program, the test for whether the final node in the path is a member of the set of nodes already reached (and hence a cheapest path has already been found) is made only when the path is taken from the priority queue.
A formulation which is closer to Dijkstra's original
keeps two sets of nodes, associated with each node is the cost
of a path to it and the node's predecessor in the path. The first set,
nodes1 is the set of those nodes where we know the
cheapest path to them, and the associated cost and predecessor will
be the cost of the cheapest path to that node and the node's predecessor
in that path. The second set, nodes2 is those nodes where
although a path has been found to them it may not be the cheapest path.
The set nodes2 is equivalent to the priority queue in the
formulation above. The difference here is that if a cheaper path to
a given node is found, instead of a new entry being made into a priority
queue of paths, the entry for the destination node in the set
nodes2 is changed with the associated cost altered to the
new cheapest cost and the associated predecessor node to the predecessor
node in the new cheapest path.
At each round of the iteration, the node with the cheapest path of all
the nodes in nodes2 is removed from that set and put
in the set nodes1. Then all edges that link to it are
considered, extending the path of that node. If an edge links to a node which
is neither in nodes1 or nodes2 a new entry is
made into nodes2 with the predecessor node the node being
transferred between sets and the cost the cost of its path plus the edge
extending it to the new node. If an edge links to a node which is in
nodes2 and the new path to it is cheaper than the path
recorded in nodes2 the entry nodes2 is
changed to give this new cheaper path, with the predecessor node the
one being transferred into nodes1.
The set nodes2 could be kept as a priority queue with
its entries ordered by their associated path costs. In this case,
when an entry's cost is changed the entry would have to be sifted
up to reformat the collection into a heap. This is not done in the code
below where both sets of nodes are kept as tables whose key is the
node name. The advantage of this representation is that there are
fewer entries in the set of nodes nodes2 than there
would be in the priority queue of paths. Since the code below does not
store nodes2 in cost order, it is necessary to search through
it to find the node with the lowest cost path.
import java.io.*;
import java.util.*;
class UseCGraphs7
{
// Finds shortest path from one node to all others
// Dijkstra's algorithms
public static void main(String[] args)
throws IOException
{
BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
BufferedReader file;
System.out.print("Enter name of file for graph: ");
file = new BufferedReader(new FileReader(in.readLine().trim()));
CGraph1 graph = new CGraph1(file);
file.close();
ETable nodes1 = new ETable5();
System.out.print("Enter start node: ");
String start = in.readLine().trim();
System.out.println();
findPaths(start,graph,nodes1);
Enumeration enum = nodes1.getEnumeration();
while(enum.hasMoreElements())
{
Path p = (Path)enum.nextElement();
System.out.print("Destination: "+p.to+" Cost: "+p.cost);
System.out.println(" Route: "+getRoute(p.pred,nodes1)+p.to);
}
}
private static void findPaths(String start,CGraph1 graph,ETable nodes1)
{
ETable nodes2 = new ETable5();
nodes2.add(new Path(start,null,0));
while(true)
{
Path p;
Enumeration enum = nodes2.getEnumeration();
if(!enum.hasMoreElements())
break;
Path min = (Path)enum.nextElement();
while(enum.hasMoreElements())
{
p = (Path)enum.nextElement();
if(p.cost<min.cost)
min=p;
}
nodes1.add(min);
nodes2.delete(min.to);
enum = graph.getLinks(min.to);
while(enum.hasMoreElements())
{
Arc next = (Arc)enum.nextElement();
if(nodes1.retrieve(next.getTo())==null)
{
int cost = min.cost+next.getCost();
p = (Path)nodes2.retrieve(next.getTo());
if(p==null)
{
p = new Path(next.getTo(),min.to,min.cost+next.getCost());
nodes2.add(p);
}
else if(cost<p.cost)
{
p.cost = cost;
p.pred = min.to;
}
}
}
}
}
private static String getRoute(String to,ETable paths)
{
if(to==null)
return "";
else
{
Path p = (Path)paths.retrieve(to);
return getRoute(p.pred,paths)+to+",";
}
}
private static class Path extends KeyObject implements Comparable
{
int cost;
String to,pred;
Path(String t,String p,int c)
{
cost=c;
to=t;
pred=p;
}
public String getKey()
{
return to;
}
public int compareTo(Object obj)
{
Path p = (Path)obj;
if(cost==p.cost)
return 0;
else if(cost<p.cost)
return -1;
else
return 1;
}
}
}
In the original formulation of Dijkstra's algorithm, the set
nodes2 contains all the nodes to which the cheapest
path has not been found, with those nodes to which no path at all
has been found indicated by assigning the path cost to infinity.
Also, the nodes are named by integers, with the two sets represented
as arrays, so that if n is a node, and a
the array, then a[n] gives the cost of the path to node
n.
To see how this algorithm works, let us consider it with the graph above, working out the cheapest paths from node x. Initially we have just the empty path as the path to x, indicated by an entry whose predecessor is null:
nodes1: {}
nodes2: {(x,null,0)}
This is moved from nodes2 to nodes1 as
the cheapest path is nodes2 (it is, of course, the only
path in nodes2 at this point). Both its links go to nodes
not in nodes2 so these new entries are added, giving:
nodes1: {(x,null,0)}
nodes2: {(y,x,4),(z,x,5)}
Now the node with the cheapest path is taken from nodes2
and added to nodes1, it has just one link, to a new node
a. The cost of the link is 3, so this is added to
the 4 of the path to give 7, with y being the
node before a in the path of cost 7 from
x to a, and the new
node with this path put into nodes2 giving:
nodes1: {(x,null,0),(y,x,4)}
nodes2: {(z,x,5),(a,y,7)}
When the entry (z,x,5) is taken from
nodes2 as the node with the cheapest path there, the
only link is to a of cost 5, but this would
lead to a path of cost 9 to a which is not
cheaper than the cost of 7 recorded for the path to a
so no other change is made:
nodes1: {(x,null,0),(y,x,4),(z,x,5)}
nodes2: {(a,y,7)}
Now there is only one node in nodes2 to be taken out, but
it links to four new nodes, so that results in:
nodes1: {(x,null,0),(y,x,4),(z,x,5),(a,y,7)}
nodes2: {(l,a,11),(b,a,12),(c,a,14),(g,a,17)}
The node with the cheapest path to it in nodes2 is now
l with a path from x
of total cost 11, with last-but-one node a.
Moving this to nodes1 and adding its one link to a new
node gives:
nodes1: {(x,null,0),(y,x,4),(z,x,5),(a,y,7),(l,a,11)}
nodes2: {(b,a,12),(c,a,14),(g,a,17),(m,l,13)}
Now the path to b is the cheapest in
nodes2, and it extends to two new nodes, giving:
nodes1: {(x,null,0),(y,x,4),(z,x,5),(a,y,7),(l,a,11),(b,a,12)}
nodes2: {(c,a,14),(g,a,17),(m,l,13),(d,b,16),(e,b,18)}
Now the path to m is the cheapest, and it has one link to a new node, f giving:
nodes1: {(x,null,0),(y,x,4),(z,x,5),(a,y,7),(l,a,11),(b,a,12),(m,l,13)}
nodes2: {(c,a,14),(g,a,17),(d,b,16),(e,b,18),(f,m,16)}
The path to c of cost 14 whose second-to-last node is
a is now the cheapest path in nodes2,
so it as recognised as the cheapest possible path to c
by moving it to nodes1. It has just one outgoing link,
to e of cost 2, and adding the cost of this link to
the path to c gives a path to e
of cost 16. There is already a path to e in
nodes2, with second-to-last node d.
But its cost is 18. So the cost of the path to e
is changed to the lower 16, and the second-to-last node in that
new path is node c, resulting in:
nodes1: {(x,null,0),(y,x,4),(z,x,5),(a,y,7),(l,a,11),(b,a,12),(m,l,13),(c,a,14)}
nodes2: {(g,a,17),(d,b,16),(e,c,16),(f,m,16)}
At this point, we have the cheapest paths, each of cost 16, to
d, e and f.
It does not matter in which order they are taken. If f
is taken first, there are no outgoing links, so we get:
Then the only outgoing link from e is to
f which is now in
Similar applies to d giving:
Node g leads to new node h,
giving:
This node is the only one in
The next step gives a path to k with second to
last node j:
But the step after this finds a cheaper path to k,
with seocnd-to-last node i of cost 29:
The only edge leading from node k is to
node f which is in
When
Last modified: 30 November 2001
nodes1: {(x,null,0),(y,x,4),(z,x,5),(a,y,7),(l,a,11),(b,a,12),(m,l,13),(c,a,14),(f,m,16)}
nodes2: {(g,a,17),(d,b,16),(e,c,16)}
nodes2 so it
isn't considered, giving:
nodes1: {(x,null,0),(y,x,4),(z,x,5),(a,y,7),(l,a,11),(b,a,12),(m,l,13),(c,a,14),(f,m,16),(e,c,16)}
nodes2: {(g,a,17),(d,b,16)}
nodes1: {(x,null,0),(y,x,4),(z,x,5),(a,y,7),(l,a,11),(b,a,12),(m,l,13),(c,a,14),(f,m,16),(e,c,16),(d,b,16)}
nodes2: {(g,a,17)}
nodes1: {(x,null,0),(y,x,4),(z,x,5),(a,y,7),(l,a,11),(b,a,12),(m,l,13),(c,a,14),(f,m,16),(e,c,16),(d,b,16),(g,a,17)}
nodes2: {(h,g,22)}
nodes2 so its path is immediately
taken as the cheapest path to ot, and extended by its two outgoing links
giving:
nodes1: {(x,null,0),(y,x,4),(z,x,5),(a,y,7),(l,a,11),(b,a,12),(m,l,13),(c,a,14),(f,m,16),(e,c,16),(d,b,16),(g,a,17),(h,g,22)}
nodes2: {(i,h,25),(j,h,24)}
nodes1: {(x,null,0),(y,x,4),(z,x,5),(a,y,7),(l,a,11),(b,a,12),(m,l,13),(c,a,14),(f,m,16),(e,c,16),(d,b,16),(g,a,17),(h,g,22),(j,h,24)}
nodes2: {(i,h,25),(k,j,30)}
nodes1: {(x,null,0),(y,x,4),(z,x,5),(a,y,7),(l,a,11),(b,a,12),(m,l,13),(c,a,14),(f,m,16),(e,c,16),(d,b,16),(g,a,17),(h,g,22),(j,h,24),(i,h,25)}
nodes2: {(k,i,29)}
nodes1,
so when k is taken from nodes2 to
nodes1 it leaves nodes2 empty:
nodes1: {(x,null,0),(y,x,4),(z,x,5),(a,y,7),(l,a,11),(b,a,12),(m,l,13),(c,a,14),(f,m,16),(e,c,16),(d,b,16),(g,a,17),(h,g,22),(j,h,24),(i,h,25),(k,i,29)}
nodes2: {}
nodes2 is empty, the algorithm terminates.
Matthew Huntbach